Quicksort!

Why are there so many sorting methods? Why don’t we just settle on the best and use it and skip the rest?

This is a good question and the answer is that different sorts work better under different numbers of elements, with different requirements of memory space, and with different levels of stability. Stability is a concept we’ll consider later. For now, make a mental note that our current subject, Quicksort, is unstable. This is a negative quality in some cases. But Quicksort is also very fast — so sometimes we will use it anyway. And system hybrid sort methods might use it as one member of an collect of sort algorithms that get called depending on the conditions.

With Quicksort, also a recursive sort, we do the recursion after we do the partitioning. Mergesort did the recursion before it did the partitioning.

The basic idea is this:

1. Shuffle the array. This is important.

2. Partition the array.

1. Arbitrarily choose a partitioning point. Call it ‘lo’ But since it’s arbitrary, let’s choose the first element in the array.

2. Next set two more index points, called i and j. Set i to be lo + 1, so that it’s right next to the lo index. Set j to be at the end of the array, or count – 1.

3. Move i from left to right as long as a[i] < a[lo]

4. Move j from right to left as long as a[j] > a[lo]

5. When you reach the stopping point for both i and j, then exchange those two elements.

6. Continue this until j crosses i.

7. Exchange the values at j and lo

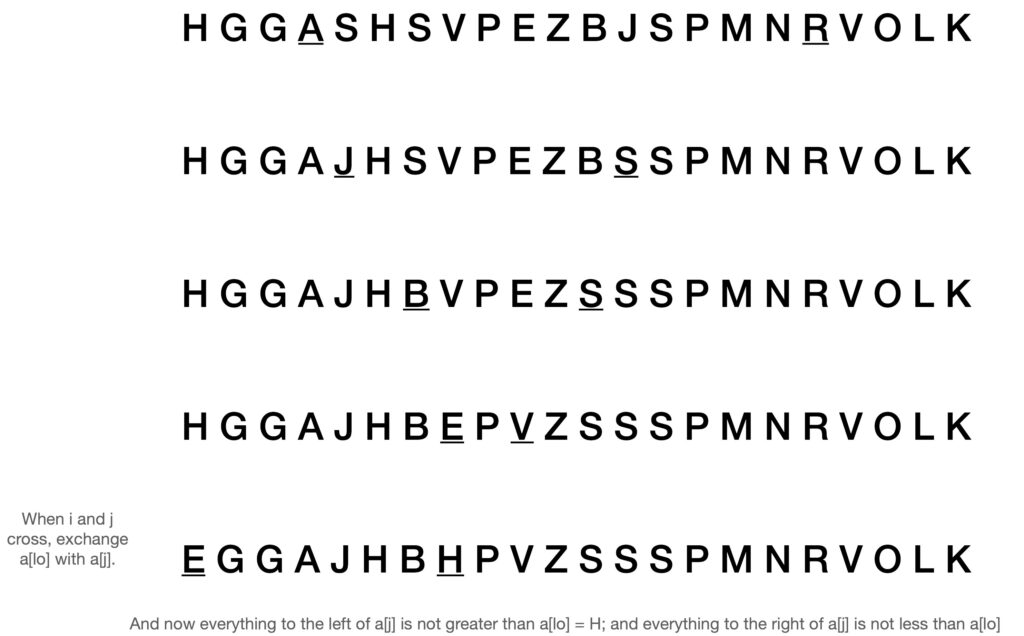
After the above:

3. Sort each partition recursively. This means sort the left partition from lo to j recursively and sort the right partition from j to i recursively.

4. That’s it.

Note that one of the advantages of Quicksort over Mergesort is that it does the sorting in place — you don’t need to create an auxiliary array.

The shuffle is important for performance. And the resulting speed of Quicksort shows this. Without the shuffle, the performance is decreased.

Both Mergesort and Quicksort are O(n lg n) sorts. But Quicksort is 30-40% faster than mergesort.

The average case analysis of Quicksort  — where the elements are shuffled — is the case with the greatest performance. In this case, the number of comparisons performed by Quicksort is 1.39*(n lg n).

In fact, this is about 39% more compares than Mergesort. But Quicksort only moves a pointer after the partitioning. Mergesort has to move items from an aux array, and this is more time consuming.

Here’s the code for Quicksort — including the partitioning code:

func quickSort(array: [Double]) -> [Double] {

    var a = knuthShuffle(a: array)

    quickSort(a: &a, lo: 0, hi: a.count – 1)

    return a

}

func quickSort(a: inout [Double], lo: Int, hi: Int) {

    if hi <= lo {

        return

    }

    let j = quickSortPartition(a: &a, lo: lo, hi: hi)

    quickSort(a: &a, lo: lo, hi: j – 1)

    quickSort(a: &a, lo: j+1, hi: hi)

}

func quickSortPartition(a: inout [Double], lo: Int, hi: Int) -> Int {

    var i = lo

    var j = hi + 1

    while(true) {

        i += 1

        while (a[i] < a[lo]) {

            if i == hi {

                break

            }

            i += 1

        }

        j -= 1

        while a[lo] < a[j] {

            if j == lo {

                break

            }

            j -= 1

        }

        if i >= j {

            break

        }

        a = exchange(a: a, i: i, j: j)

    }

    a = exchange(a: a, i: lo, j: j)

    return j

}